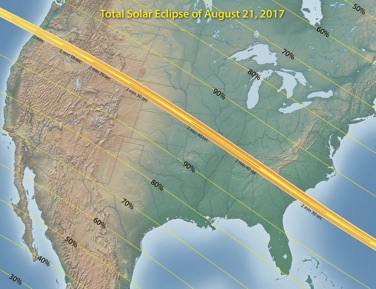
- Press the Run Time Forward button to see how the Moon’s shadow travels from the Pacific coast to the Atlantic coast.
Calculating the Speed of the Lunar Shadow on the Earth
- Average Speed in the West: The total solar eclipse starts at Madras, Oregon at 17:19:37.9 UT. The total eclipse will start 741 km further east at Idaho Falls, Idaho at 17:32:59.6 UT. Calculate the average speed of the Moon’s shadow in the western U.S. as it travels between Madras and Idaho Falls. Total travel time between Madras and Idaho Falls = 13:21.7 min = 13.362 min ≈0.223 h
- Average Speed in the East: The total solar eclipse starts at Nashville, Tennessee at 18:27:29.2 UT. The total eclipse will start 578 km further east at Columbia, South Carolina at 18:41:49.6 UT. Calculate the average speed of the Moon’s shadow in the eastern U.S. as it travels between Nashville and Columbia. Average speed = (total distance) / (total time) = 578 km / 0.239 h ≈ 2,420 km/h
- You should notice that the average speeds are not the same. Why should the average speed of the lunar shadow vary as the umbra travels from the west coast to the east coast of the U.S.? The speed of the umbra is connected to the Earth’s orbital motion. The umbra would be at its slowest near the equator because the Earth’s speed of rotation is fastest there. Increasing latitude leads to an increase in the umbra’s speed as the Earth’s speed of rotation gradually decreases. The August 21, 2017 eclipse shadow gradually travels south as the umbra travels from the west coast to the east coast of the U.S.; this results in a gradual decrease in the umbra’s speed.
Average speed = (total distance) / (total time) = 741 km / 0.223 h ≈ 3,320 km/h
The average speed of the Moon’s shadow in the west is approximately 3,320 km/h (i.e. 2,060 mph).
The average speed of the Moon’s shadow in the east is approximately 2,420 km/h (i.e. 1,500 mph).
Calculating the Radius of the Lunar Shadow on the Earth
- Click here and press the Run Time Forward button to track the umbra as it travels towards the east coast. (Note: The area of the umbra is marked by a yellow circle.)
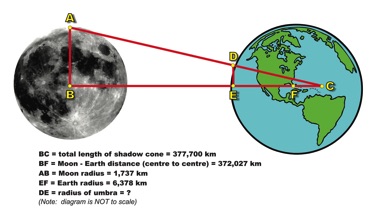
The diagram below represents the Moon-Earth geometry during the August 21, 2017 solar eclipse. Notice that the geometric length of the shadow cone, BC, actually extends well beneath the Earth’s surface, even going past the centre point of the Earth located at point F. The intersection of this shadow cone at the Earth’s surface, DE, represents the radius of the umbra on the Earth’s surface.
- Use the information contained in the diagram above to calculate the diameter of the umbra on the Earth’s surface.
∆ABC and ∆DEC are similar triangles (angle-angle similarity). We can, therefore, write:
AB/BC = DE/EC or DE = ((AB)(EC))/BC
EC = (BC- BF) + EF
= (377,700 km - 372,027 km) + 6,378 km
= 5,673 km + 6,378 km
= 12,051 km
Substituting this value for EC into our original equation will allow us to determine DE, the radius of the umbra.
DE = (AB)(EC) / BC
= (1,737 km)(12,051 km) / (377,700 km)
≈ 55.42 km
This gives a diameter for the umbra of approximately 110.8 km (i.e. diameter equals two times the radius). (NOTE: This method only provides an approximation of the umbra diameter, yet it is, nonetheless, still quite accurate. More detailed calculations predict that the actual umbra diameter near Carbondale, Illinois at the midpoint of the 2017 solar eclipse will be 115 km; this is quite close to our approximation of 110.8 km)