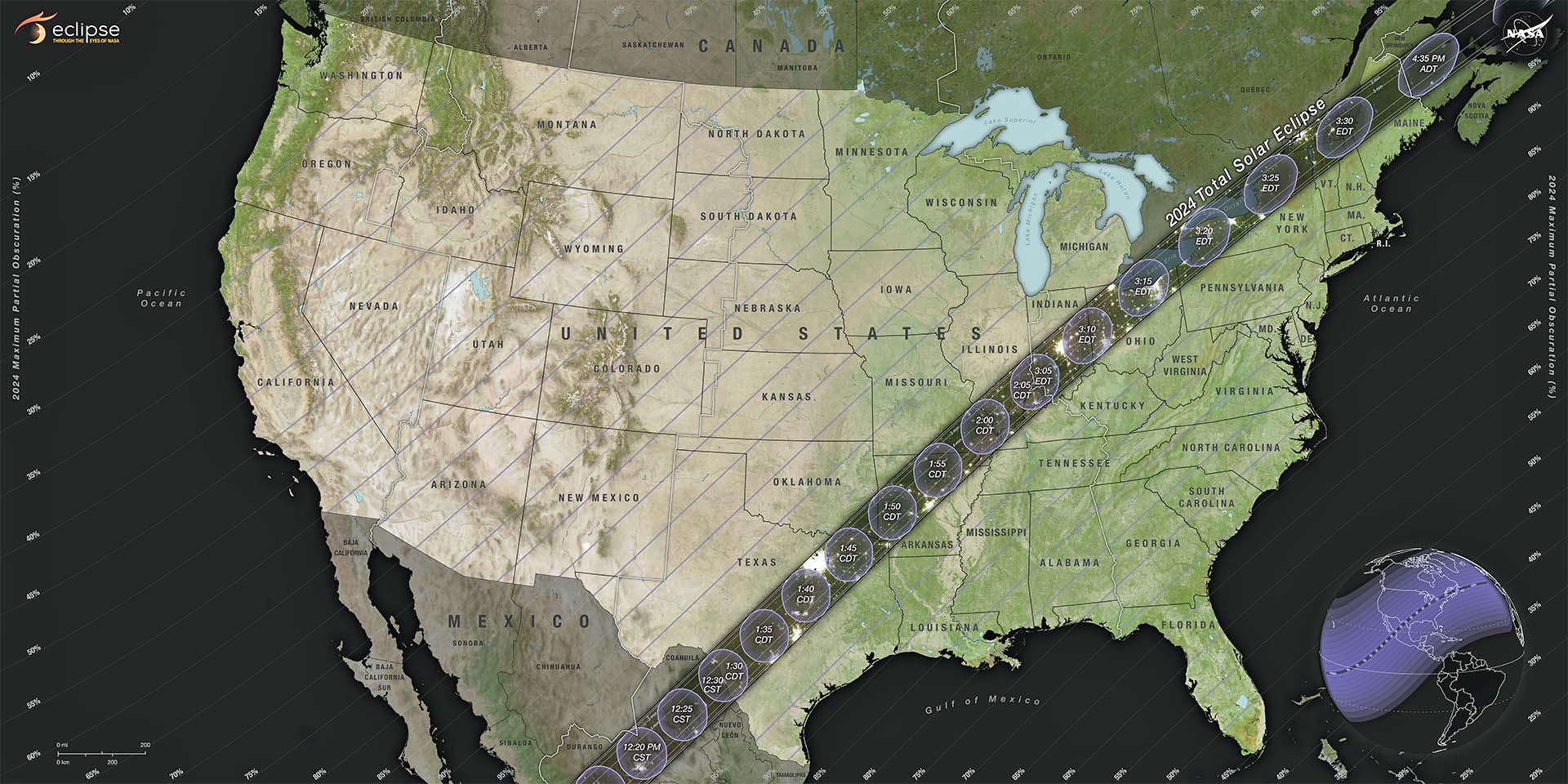
The view to the right in the main panel for April 8, 2024 shows how the umbra is formed by the shadow of the moon; yellow circles highlight the area of the umbra and the penumbra.
- Press the Run Time Forward button to see how the Moon’s shadow travels across the North American continent starting in the Pacific Ocean and ending in the Atlantic Ocean.
Calculating the Speed of the Lunar Shadow on the Earth
A solar eclipse is an excellent opportunity to do some basic Math calculations. You will use actual dates, times, and locations from the last solar eclipse in 2017 in our calculations.
- Average Speed Across the Continental U.S. A.: Totality will start at Austin, Texas at 18:36:07 UT. Totality will start in the northern part of the U.S. at Watertown, New York at 19:22:35 UT. The distance between Austin in the south and Watertown in the north is approximately 2,446 km. Use this information to calculate the average speed of the umbra, and thereby the Moon’s shadow, as it travels south to north across the continental United States. Total travel time between Austin and Watertown = 46 min 28 seconds ≈ 46.47 min ≈ 0.775 h
- Average Speed in the South: The total solar eclipse will start at Austin, Texas at 18:36:07 UT. Totality will start 502 km further northeast at Texarkana, Texas at 18:46:56 UT. Calculate the average speed of the Moon’s shadow in the southern U.S. as it travels between Austin and Texarkana. Total travel time between Austin and Texarkana = 10 min 49 seconds ≈ 10.8 min ≈ 0.180 h
- Average Speed in the North: The total solar eclipse starts at Cleveland, Ohio at 19:13:46 UT. Totality will start 547 km further northeast at Watertown, New York at 19:22:35 UT. Calculate the average speed of the Moon’s shadow in the northern U.S. as it travels between Cleveland and Watertown. Total travel time between Cleveland and Watertown = 8 min 49 seconds ≈ 8.82 min ≈ 0.147 h
- The umbra’s path gradually takes it north as the Moon’s shadow travels from the west to the east across the continental U.S..You should notice that the average speeds are not the same. The average speed of the umbra in the north is greater than its average speed in the south. Calculating the average speed across the entire U.S. (i.e. section a)) disguises this distinction. Why should the average speed of the lunar shadow vary as the umbra travels from the south to the north as it travels across the U.S.? The speed of the umbra is connected to the Earth’s orbital motion. The umbra would be at its slowest near the equator because the Earth’s speed of rotation is fastest there. Increasing latitude leads to an increase in the umbra’s speed as the Earth’s speed of rotation gradually decreases. The April 8, 2024 eclipse shadow gradually travels north as the umbra travels from Mexico through the United States and eventually into Atlantic Canada.; this increase in latitude results in a gradual increase in the umbra’s speed.
Average speed = (total distance) / (total time) = 2,446 km /0.775 h ≈ 3,160 km/h
The average speed of the Moon’s shadow as it travels across the breadth of the United States is approximately 3,160 km/h (i.e. 1,960 mph).
Calculating the average speed across the entire U.S., however, disguises an important property of the speed of the Moon’s shadow during a total solar eclipse. Sections b) and c) below address this particular aspect about the speed of the Moon’s shadow.
Average speed = (total distance) / (total time) = 502 km / 0.0.180 h ≈ 2,790 km/h
The average speed of the Moon’s shadow in the west was approximately 2,790 km/h (i.e. 1,730 mph).
Average speed = (total distance) / (total time) = 547 km / 0.147 h ≈ 3,720 km/h
The average speed of the Moon’s shadow in the east is approximately 3,720 km/h (i.e. 2,310 mph).
Calculating the Diameter of the Lunar Shadow on the Earth
- Click here and press the Run Time Forward button to track the umbra as it travels across the United States. (Note: The area of the umbra is marked by a yellow circle.)
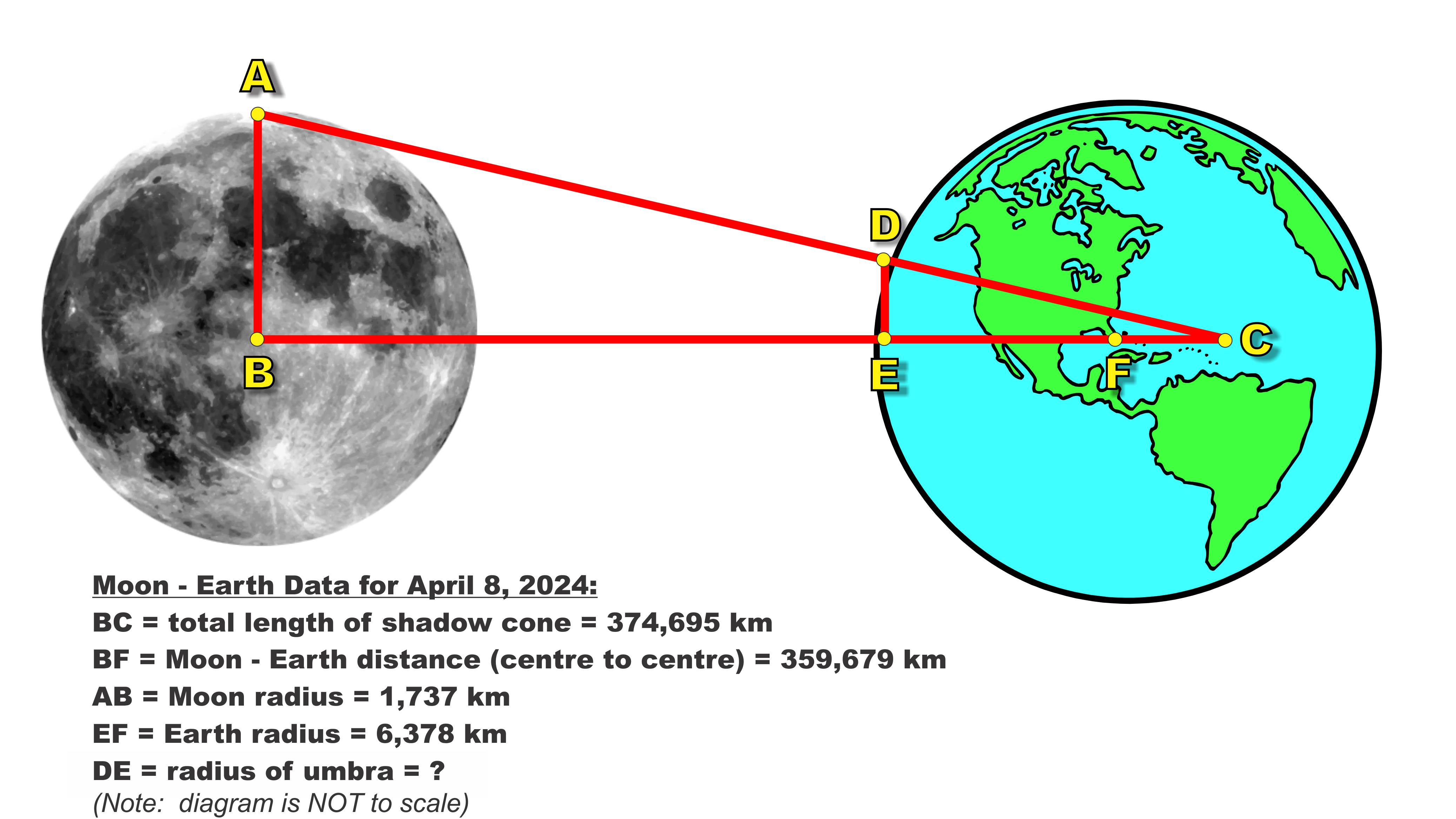
The diagram below represents the Moon- Earth geometry during the April 8, 2024 solar eclipse. Notice that the geometric length of the shadow cone, BC, actually extends well beneath the Earth’s surface, even going past the centre point of the Earth located at point F. The intersection of this shadow cone at the Earth’s surface, DE, represents the radius of the umbra on the Earth’s surface. Use the information contained in this diagram to calculate the diameter of the umbra on the Earth’s surface.
- Use the information contained in the diagram above to calculate the diameter of the umbra on the Earth’s surface.
∆ABC and ∆DEC are similar triangles (angle-angle similarity). We can, therefore, write:
AB/BC = DE/EC or DE = ((AB)(EC))/BC
Since AB (Moon radius) and BC (total length of shadow cone) are given, that only leaves EC to be determined. From the diagram we can see that:
EC = (BC- BF) + EF
= (374,695 km - 359,679 km) + 6,378 km
= 15,016 km + 6,378 km
= 21,394 km
Substituting this value for EC into our original equation will allow us to determine DE, the radius of the umbra.
DE = (AB)(EC) / BC
= (1,737 km)(21,394 km) / (374,695 km)
≈ 55.42 km
This gives a diameter for the umbra of approximately 99.2 km (i.e. diameter equals two times the radius). (NOTE: This method only provides an approximation of the umbra diameter, yet it is, nonetheless, still quite accurate. More detailed calculations predict that the actual maximum diameter of the unbra as it travels across the U.S. will be approximately 198 km; this is quite close to our calculated value of 198.4 km)
Solar Eclipse Shadow Play Activity
Download and print out this activity worksheet to help understand the mechanics and phenomena of a solar eclipse using simple hands-on materials, without directly observing the sun.