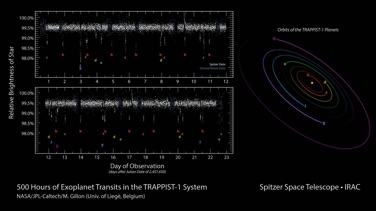
Apart from a few special exceptions, directly observing planets hidden in the glare of their stars is beyond our current technology. So we have to rely on indirect methods to detect and characterize them. By far, the easiest methods involve measuring the small effects that the planets have on their star. The most fruitful of these techniques has been Transit Photometry - measuring the dimming of a star’s light when its planets pass between us and the star. Radial Velocity and Stellar Astrometry are other methods that detect the subtle motions of stars caused by orbiting planets tugging on them gravitationally. The TRAPPIST-1 discovery used the transit method.
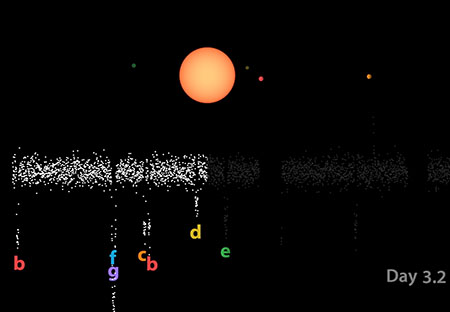
Transit methods only work for the small percentage of star systems that are oriented edge-on towards Earth. Fortunately, that’s still a lot of stars! On a regular interval each planet transits the disk of its star, temporarily causing a slight reduction of the star’s light (on the order of 1 part in 10,000) as viewed from Earth. The amount of the reduction is proportional to the size of the planet. The dip re-occurs every time the planet completes an orbit. By recording the brightness of the starlight continuously over a long period of time, we can determine the length of a planet’s year and the radius of its orbit.
The graphs of starlight versus time, known as light curves, can be complex if multiple planets are transiting – each with a different dip amount, duration, and interval – all summed together. Many stars exhibit inherent variability in their brightness, too, but the exoplanet transit dips are usually brief by comparison.
Small, Earth-sized planets produce tiny dips in light intensity. If a star is being examined using a ground-based telescope, daytime prevents continuous measurements, and atmospheric interference (i.e., twinkling) adds noise to the light curve, limiting the sensitivity and preventing the detection of small planets. To overcome this, observatories such as the Kepler Space Telescope are launched into orbit. They detect and characterize exoplanets, especially Earth-like ones, by using Transit Photometry continuously on a single small patch of sky. Kepler has discovered thousands of exoplanets, including many hot Jupiters and Neptune-sized planets, and a good number of Earth-sized planets. The Spitzer space telescope is another space-based observatory that was originally launched as an infrared observatory. With its primary mission long completed, and some of its instruments no longer operational, it is still functional as an exoplanet observer.
The time taken for the transit yields the speed of the planet, and the time interval between transits provides its orbital period (its year). These parameters allow the orbit to be calculated using laws of orbital dynamics, including the planet’s mass and its distance from the star. The amount that the host star’s light diminishes while an exoplanet transits gives astronomers the diameter of the exoplanet. Knowing its diameter and mass provides its density.
Combined with the star’s luminosity and spectral type, astronomers estimate the surface temperature of the planet. Moreover, if an exoplanet has a translucent atmosphere, or is a gas world, the reduction in light drops gradually, while one that is rocky and airless diminishes more abruptly.
The First Exoplanet
It was only in 1992 that astronomers Aleksander Wolszczan and Dale Frail confirmed the first exoplanets, found in orbit around the pulsar PSR B1257+12. Astronomers starting looking around other pulsars but it turned out that pulsar planets are very rare, with only one other pulsar planet being confirmed as of the year 2017.
Pulsars also emit too much radiation to allow the existence of organic life, so scientists continued looking for proof of other planets orbiting stars like our own, where life might have a chance to emerge and thrive. Astronomers Michel Mayor and Didier Queloz found the first exoplanet orbiting a Sun-like star in 1995 - 51 Pegasi b - 50.9 light-years from Earth in the constellation Pegasus.
Calculating TRAPPIST-1 Planet Densities
To calculate the average density of a sphere (ρ), you simply divide the mass (m) of the sphere by it’s volume (v).
ρ=m/v
If you have the radius of the sphere (r), then the volume is given by the formula:
v=(4/3)πr3For example, the mass of Earth is 5.972 × 1024 kg. To find the volume of Earth we use the formula v=(4/3)πr3. Earth's radius is 6.371 × 106 meters. Therefore, volume = (4/3)(3.14)(6.371 × 106 m)3 = 1.083 × 1021 m3. Then to find the density we divide mass by volume = 5.972 × 1024 kg/1.083 × 1021 m3 = 5514 kg/m3 = 5.51 g/cm3.
The density of water is 1 g/cm3. Planets with a density of less than 1 g/cm3 would float if dropped in a giant bathtub!
Use the table below to calculate the approximate densities for the 7 Earth-like worlds of the TRAPPIST-1 System.
| Planet | Radius | Mass | Density |
| TRAPPIST-1b | 6.94 x 106 m | 5.076 × 1024 kg | 3.63 g/cm3 |
| TRAPPIST-1c | 6.75 x 106 m | 8.24 × 1024 kg | 6.45 g/cm3 |
| TRAPPIST-1d | 4.90 x 106 m | 2.45 × 1024 kg | 4.90 g/cm3 |
| TRAPPIST-1e | 5.86 x 106 m | 3.70 × 1024 kg | 4.41 g/cm3 |
| TRAPPIST-1f | 6.63 x 106 m | 4.06 × 1024 kg | 3.31 g/cm3 |
| TRAPPIST-1g | 7.20 x 106 m | 8.00 × 1024 kg | 5.18 g/cm3 |
| TRAPPIST-1h | 4.84 x 106 m | unknown | unknown |